Constant Q Profiles and
Toroidal Models of Inter-Key Relations (ToMIR)

Benjamin Blankertz, Hendrik Purwins and Klaus Obermayer

[Abstract: gzipped ps-file  or pdf-file]
 

Emergance of ToMIR from psychoacoustic experiments and analysis of western tonal music

                

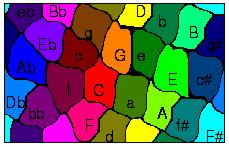
The torus on the left is a geometric representation of the inter-key relations of all major and minor keys, derived from psychoacoustic experiments by Krumhansl and Kessler [1] (shown in 3-dimensional representation). The torus on the right was derived solely from Alfred Cortot's recording of the Chopin preludes, op. 28 by the technique of constant Q profiles. (shown in 2-dimensional representation: identify left and right border and upper and lower border).

Deriving a ToMIR from basic harmonic relations


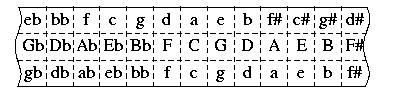
Strip of key, derived from Arnold Schoenberg's charts of key regions [2]


First Step (The strip is shown somewhat strechted for better display)


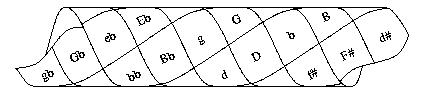
Second step: Double appearences of minor keys are brought to accordance

The borders of the tube show keys that are enharmonically equal. These are united by bending the tube and glewing together its ends. This gives a toroid surface around which the circles of fifths for major and minor keys wrap three times before joining themselves.
 

[1] C.L. Krumhansl and E.J. Kessler (1982), Tracing the dynamic changes in perceived tonal organization in a spatial representation of musical
              keys, Psychological Review Vol. 89, No. 4, 334-368.

[2] A. Schoenberg (1969), Structural functions of harmony, 2. edition, Norton, New York.

This material is part of a talk presented at

mail to: <blanker@math.uni-muenster.de>  go to: dsp-page go to: home-page